daej

　Downloadから最新版のdaejのjarファイルをダウンロードしてください。 ダウンロードしたjarファイルを各自の環境に合わせてインポートして利用できるようにしてください。

　ここからは例題を用いて説明します。用いる例題は以下の図の線形陰的なDAEで表される振り子の問題です。


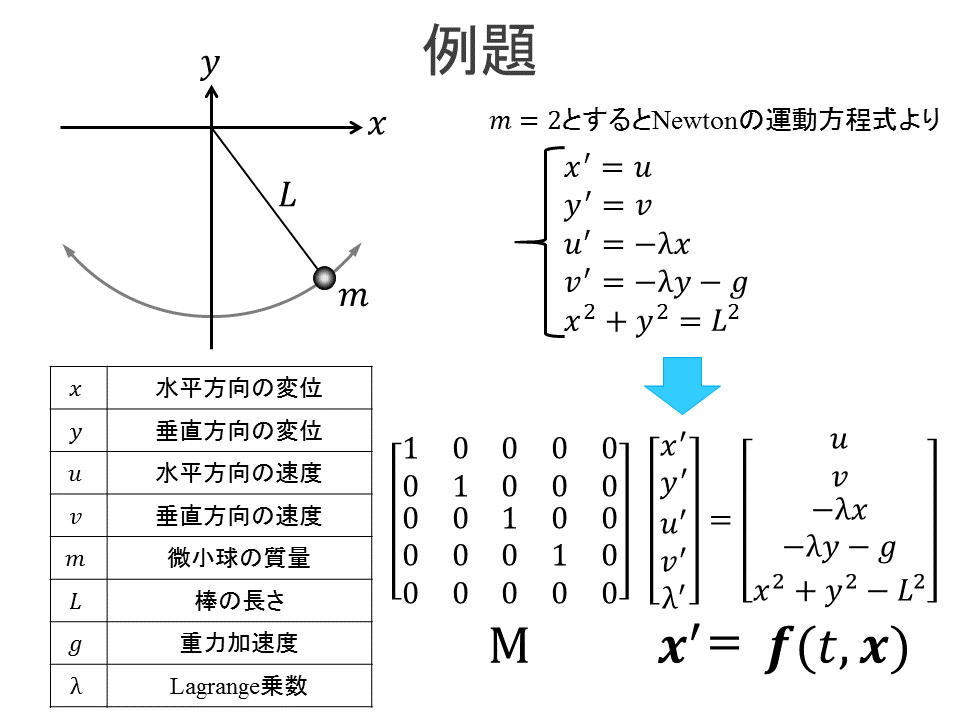
　上記の問題を解くために必要な情報として各変数の指数、初期条件(初期値、初期微分値)、各物理定数の値、各シミュレーションパラメーターを決定します。



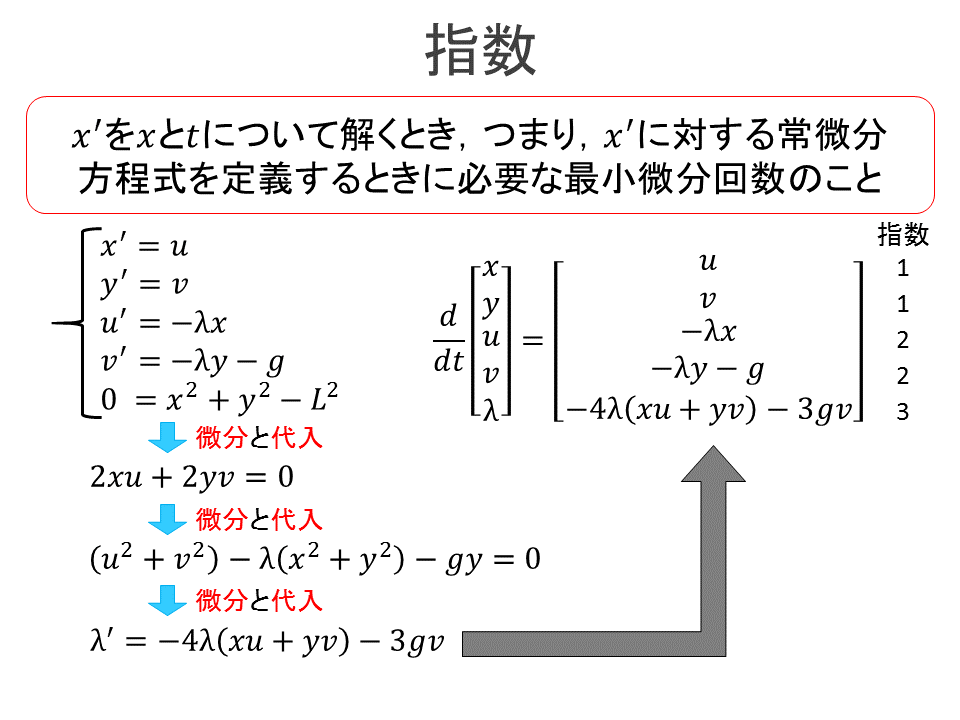
　以上の情報を用いてdaejで問題クラスを作成します。 問題クラスの作成ではorg.mklab.daej.ivps.AbstractIvpsDifferentialAlgebraicEquationを継承して問題クラスを実装します。 以下に主要なコードを記載します。ソースコードはDownloadのdaej sampleにあります。

　コンストラクタ

  public Pendulum() {
    this.fullnm = "Pendulum";   //　問題名
    this.problm = "pend";       //　問題の略称
    this.type = "DAE";          //　問題の種類
    this.numberOfEquation = 5;  //　方程式の数

    this.numjac = false;    //　ヤコビ行列を定義するか(falseで定義する)
    this.mljac = this.numberOfEquation;     //　ヤコビ行列の下バンド幅
    this.mujac = this.numberOfEquation;     //　ヤコビ行列の上バンド幅
    this.mlmas = this.numberOfEquation;     //　M行列の下バンド幅
    this.mumas = this.numberOfEquation;     //　M行列の上バンド幅

    this.ind = new int[] {1, 1, 2, 2, 3};   //　各変数の指数
    for (int i = 0; i < this.ind.length; i++)
      this.getInd()[i] = this.ind[i];
  }
								

　初期化メソッド

  public void init(int neqn, double t, double[] y, double[] yprime, boolean[] consis) {
    // 初期値
    y[0] = 1.0;
    y[1] = 0.0;
    y[2] = 0.0;
    y[3] = 1.0;
    y[4] = 1.0;

    //　初期微分値
    yprime[0] = 0.0;
    yprime[1] = 1.0;
    yprime[2] = -1.0;
    yprime[3] = -9.8;
    yprime[4] = 3 * 9.8;

    consis[0] = true;
  }
								

　f(t,x)の記述

  public void feval(int neqn, double t, double[] y, double[] yprime, double[] f, int[] ierr, double[] rpar, int[] ipar) {
    // f(t,x)
    f[0] = y[2];
    f[1] = y[3];
    f[2] = -y[4] * y[0];
    f[3] = -y[4] * y[1] - 9.8;
    f[4] = y[0] * y[0] + y[1] * y[1] - 1;
  }
								

　ヤコビ行列Jの設定

  public void jeval(int ldim, int neqn, double t, double[] y, double[] yprime, double[][] dfdy, int[] ierr, double[] rpar, int[] ipar) {
    // ヤコビ行列J
    dfdy[0][2] = 1.0;
    dfdy[1][3] = 1.0;
    dfdy[2][0] = -y[4];
    dfdy[2][4] = -y[0];
    dfdy[3][1] = -y[4];
    dfdy[3][4] = -y[1];
    dfdy[4][0] = 2 * y[0];
    dfdy[4][1] = 2 * y[1];
  }
								

　行列Mの設定

  public void meval(int ldim, int neqn, double t, double[] y, double[] yprime, double[][] dfddy, int[] ierr, double[] rpar, int[] ipar) {
    // M行列
    dfddy[0][0] = 1.0;
    dfddy[1][1] = 1.0;
    dfddy[2][2] = 1.0;
    dfddy[3][3] = 1.0;
  }
								

　続いてシミュレーションのためのメインクラスを作成します。

メインメソッド

  public static void main(String[] args) {
    //　問題クラスを生成
    IvpsDaejDifferentialAlgebraicEquation problem = new Pendulum();

    //　解を求める時刻の設定
    final double[] t = {0.0, 10.0};

    //　ソルバーのドライバークラスを生成
    IvpsDaejDifferentialAlgebraicEquationSolver solver = new IvpsBimdd(problem);
    // シミュレーションパラメーターの設定
    solver.setAbsoluteTolerance(1e-8);
    solver.setRelativeTolerance(1e-8);
    solver.setInitialStepSize(1e-8);

    // 問題を解く
    solver.solve(t);

    //　解を取得
    double[][] result = solver.getSolution();

    // 解を表示
    System.out.println("実行結果");
    for (int i = 0; i < result.length; i++) {
      for (int j = 0; j < result[0].length; j++) {
        Double ty = new Double(result[i][j]);
        String str = String.format("%15e ", ty);
        System.out.print(str);
      }
      System.out.println("");
    }
  }
								

　シミュレーション完了すると以下のようなシミュレーション結果を得られます。

出力結果

  実行結果
     0.000000e+00    1.000000e+01 
     1.000000e+00    9.163574e-01 
     0.000000e+00   -4.003611e-01 
     0.000000e+00   -1.190799e+00 
     1.000000e+00   -2.725532e+00 
     1.000000e+00    1.277011e+01 
								

　一行目が初期時刻と終了時刻、二行目以降が初期時刻と終了時刻における各変数(x,y,u,v,λ)の値です。